For published studies, this command calculates (1) how much bias there must be in an estimate to nullify/sustain an inference; (2) the impact of an omitted variable necessary to nullify/sustain an inference for a regression coefficient. For a full description of the command’s usage and additional examples, please refer to our practical guide.
Usage
pkonfound(
est_eff,
std_err,
n_obs,
n_covariates = 1,
alpha = 0.05,
tails = 2,
index = "RIR",
nu = 0,
n_treat = NULL,
switch_trm = TRUE,
model_type = "ols",
a = NULL,
b = NULL,
c = NULL,
d = NULL,
two_by_two_table = NULL,
test = "fisher",
replace = "control",
sdx = NA,
sdy = NA,
R2 = NA,
far_bound = 0,
eff_thr = NA,
FR2max = 0,
FR2max_multiplier = 1.3,
to_return = "print",
upper_bound = NULL,
lower_bound = NULL,
raw_treatment_success = NULL,
replace_stu = NULL,
peer_effect_pi = 0.5
)Arguments
- est_eff
the estimated effect (e.g., an unstandardized beta coefficient or a group mean difference).
- std_err
the standard error of the estimate of the unstandardized regression coefficient.
- n_obs
the number of observations in the sample.
- n_covariates
the number of covariates in the regression model.
- alpha
the probability of rejecting the null hypothesis (defaults to 0.05).
- tails
integer indicating if the test is one-tailed (1) or two-tailed (2; defaults to 2).
- index
specifies whether output is RIR or IT (impact threshold); defaults to
"RIR".- nu
specifies the hypothesis to be tested; defaults to testing whether
est_effis significantly different from 0.- n_treat
the number of cases associated with the treatment condition (for logistic regression models).
- switch_trm
indicates whether to switch the treatment and control cases; defaults to
FALSE.- model_type
the type of model; defaults to
"ols", but can be set to"logistic".- a
the number of cases in the control group showing unsuccessful results (2x2 table model).
- b
the number of cases in the control group showing successful results (2x2 table model).
- c
the number of cases in the treatment group showing unsuccessful results (2x2 table model).
- d
the number of cases in the treatment group showing successful results (2x2 table model).
- two_by_two_table
a table (matrix, data.frame, tibble, etc.) from which
a,b,c, anddcan be extracted.- test
specifies whether to use Fisher's Exact Test (
"fisher") or a chi-square test ("chisq"); defaults to"fisher".- replace
specifies whether to use the entire sample (
"entire") or the control group ("control") for calculating the base rate; default is"control".- sdx
the standard deviation of X (used for unconditional ITCV).
- sdy
the standard deviation of Y (used for unconditional ITCV).
- R2
the unadjusted, original \(R^2\) in the observed function (used for unconditional ITCV).
- far_bound
indicates whether the estimated effect is moved to the boundary closer (0, default) or further away (1).
- eff_thr
for RIR: the unstandardized coefficient threshold to change an inference; for IT: the correlation defining the threshold for inference.
- FR2max
the largest \(R^2\) (or \(R^2_{\max}\)) in the final model with an unobserved confounder (used for COP).
- FR2max_multiplier
the multiplier applied to \(R^2\) to derive \(R^2_{\max}\); defaults to 1.3 (used for COP).
- to_return
specifies the output format:
"print"(default) to display output,"plot"for a plot, or"raw_output"to return a data.frame for further analysis.- upper_bound
optional (replaces
est_eff); the upper bound of the confidence interval.- lower_bound
optional (replaces
est_eff); the lower bound of the confidence interval.- raw_treatment_success
optional; the unadjusted count of successful outcomes in the treatment group for calculating the specific RIR benchmark.
- replace_stu
score of the hypothetical average student who replaces the original student.
- peer_effect_pi
proportion of students exerting peer effects on the others.
Details
The function accepts arguments depending on the type of model:
Linear Models (index: RIR, ITCV, PSE, COP)
est_eff, std_err, n_obs, n_covariates, alpha, tails, index, nu
sdx, sdy, R2, far_bound, eff_thr, FR2max, FR2max_multiplier
upper_bound, lower_bound
Logistic Regression Model
est_eff, std_err, n_obs, n_covariates, n_treat, alpha, tails, nu
replace, switch_trm, raw_treatment_success, model_type
2x2 Table Model (Non-linear)
a, b, c, d, two_by_two_table, test, replace, switch_trm
VAM model (beta)
est_eff, replace_stu, n_obs, eff_thr, peer_effect_pi
Note
For a thoughtful background on benchmark options for ITCV, see Cinelli & Hazlett (2020), Lonati & Wulff (2024), and Frank (2000).
Values
pkonfound prints the bias and the number of cases that would have to be replaced with cases for which there is no effect to nullify the inference. If to_return = "raw_output", a list is returned with the following components:
RIR & ITCV for linear model
obs_rcorrelation between predictor of interest (X) and outcome (Y) in the sample data
act_rcorrelation between predictor of interest (X) and outcome (Y) from the sample regression based on the t-ratio accounting for non-zero null hypothesis
critical_rcritical correlation value at which the inference would be nullified (e.g., associated with p=.05)
r_finalfinal correlation value given confounding variable (CV). Should be equal to
critical_rrxcvunconditional \(corr(X,CV)\) necessary to nullify the inference for smallest impact
rycvunconditional \(corr(Y,CV)\) necessary to nullify the inference for smallest impact
rxcvGz\(corr(X,CV|Z)\) conditioning on all observed covariates
rycvGz\(corr(Y,CV|Z)\) conditioning on all observed covariates
itcvunconditional ITCV (
uncond_rxcv * uncond_rycv)itcvGzconditional ITCV given all observed covariates
r2xz\(R^2\) using all observed covariates to explain the predictor of interest (X)
r2yz\(R^2\) using all observed covariates to explain the predictor of interest (Y)
beta_thresholdthreshold for for estimated effect
beta_threshold_verifyverified threshold matching
beta_thresholdperc_bias_to_changepercent bias to change inference
RIR_primaryRobustness of Inference to Replacement (RIR)
RIR_supplementalRIR for an extra row or column that is needed to nullify the inference
RIR_percRIR as % of total sample (for linear regression) or as % of data points in the cell where replacement takes place (for logistic and 2 by 2 table)
Fig_ITCVITCV plot object
Fig_RIRRIR threshold plot object
COP for linear model
delta*delta calculated using Oster’s unrestricted estimator
delta*restricteddelta calculated using Oster’s restricted estimator
delta_exactdelta calculated using correlation-based approach
delta_pctbiaspercent bias when comparing
delta*todelta_exactdelta_sigdelta threshold at which focal predictor loses statistical significance at the chosen
alpha(default: 0.05)rxcvGz_sigboundary partial correlation \(r_{X,\mathrm{CV} | Z}\) associated with
delta_sigrycvGz_sigboundary partial correlation \(r_{Y,\mathrm{CV} | Z}\) associated with
delta_sigvar(Y)variance of the dependent variable (\(\sigma_Y^2\))
var(X)variance of the independent variable (\(\sigma_X^2\))
var(CV)variance of the confounding variable (\(\sigma_{CV}^2\))
cor_ostercorrelation matrix implied by
delta*cor_exactcorrelation matrix implied by
delta_exacteff_x_M3_ostereffect estimate for X under the Oster‑PSE variant
eff_x_M3effect estimate for X under the PSE adjustment
Tableformatted results table
FigureCOP diagnostic plot
PSE for linear model
corr(X,CV|Z)correlation between X and CV conditional on Z
corr(Y,CV|Z)correlation between Y and CV conditional on Z
corr(X,CV)correlation between X and CV
corr(Y,CV)correlation between X and CV
covariance matrixcovariance matrix among Y, X, Z, and CV under the PSE adjustment
eff_M3estimated unstandardized regression coefficient for X in M3 under the PSE adjustment
se_M3standard error of that coefficient in M3 under the PSE adjustment
Tablematrix summarizing key statistics from three nested regression models (M1, M2, M3)
RIR for logistic model
RIR_primaryRobustness of Inference to Replacement (RIR)
RIR_supplementalRIR for an extra row or column that is needed to nullify the inference
RIR_percRIR as % of data points in the cell where replacement takes place
fragility_primaryFragility; the number of switches (e.g., treatment success to treatment failure) to nullify the inference
fragility_supplementalFragility for an extra row or column that is needed to nullify the inference
starting_tableobserved (implied) 2 by 2 table before replacement and switching
final_tablethe 2 by 2 table after replacement and switching
user_SEuser-entered standard error
analysis_SEthe standard error used to generate a plausible 2 by 2 table
needtworowsindicator whether extra switches were needed
RIR for 2×2 table model
RIR_primaryRobustness of Inference to Replacement (RIR)
RIR_supplementalRIR for an extra row or column that is needed to nullify the inference
RIR_percRIR as % of data points in the cell where replacement takes place
fragility_primaryFragility; the number of switches (e.g., treatment success to treatment failure) to nullify the inference
fragility_supplementalFragility for an extra row or column that is needed to nullify the inference
starting_tableobserved 2 by 2 table before replacement and switching
final_tablethe 2 by 2 table after replacement and switching
needtworowsindicator whether extra switches were needed
Examples
## Linear models
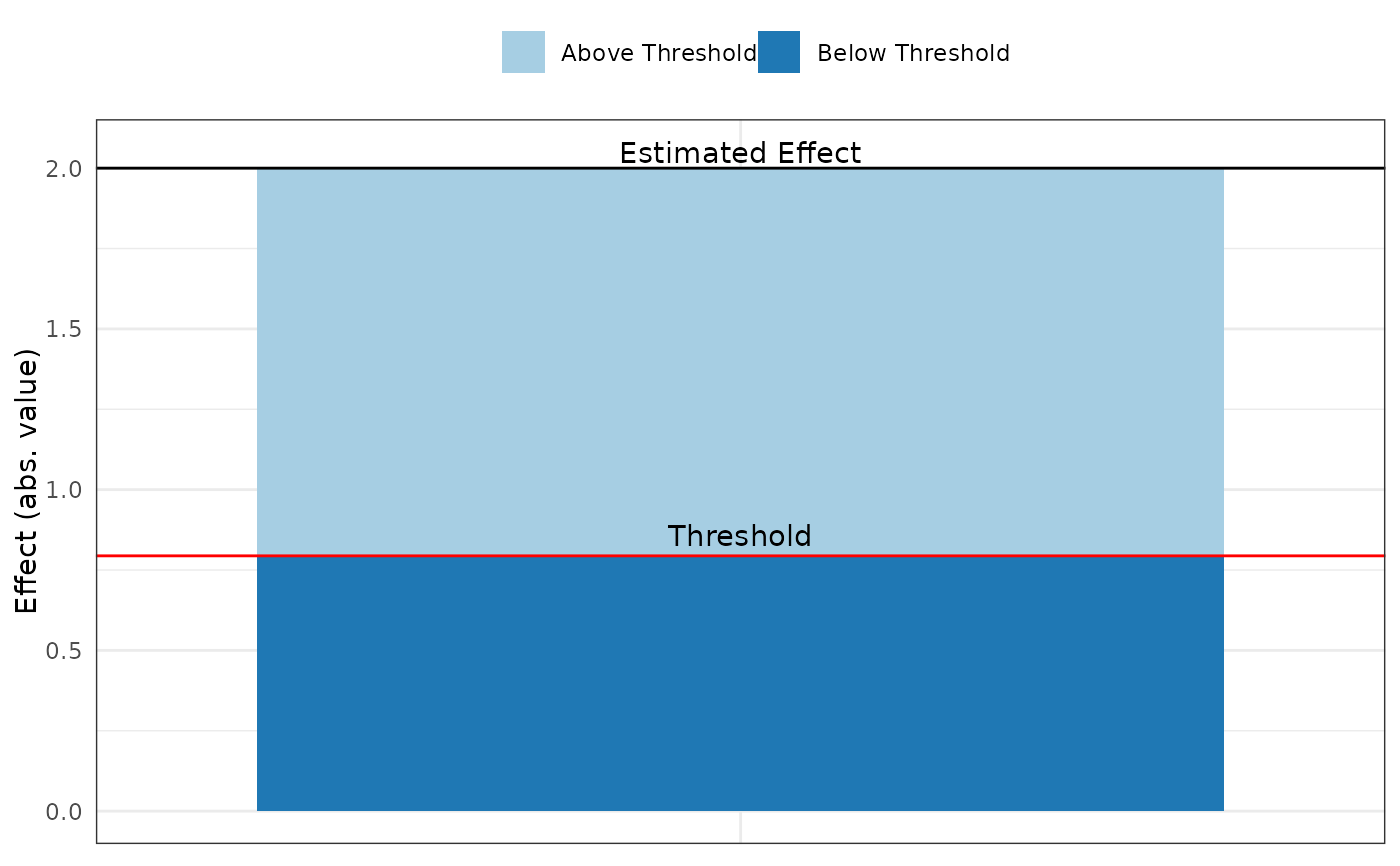
pkonfound(2, .4, 100, 3)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 60
#>
#> To nullify the inference of an effect using the threshold of 0.794 for
#> statistical significance (with null hypothesis = 0 and alpha = 0.05), 60.295%
#> of the estimate of 2 would have to be due to bias. This implies that to
#> nullify the inference one would expect to have to replace 60 (60.295%)
#> observations with data points for which the effect is 0 (RIR = 60).
#>
#> See Frank et al. (2013) for a description of the method.
#>
#> Citation: Frank, K.A., Maroulis, S., Duong, M., and Kelcey, B. (2013).
#> What would it take to change an inference?
#> Using Rubin's causal model to interpret the robustness of causal inferences.
#> Education, Evaluation and Policy Analysis, 35 437-460.
#>
#> Accuracy of results increases with the number of decimals reported.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(-2.2, .65, 200, 3)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 83
#>
#> To nullify the inference of an effect using the threshold of -1.282 for
#> statistical significance (with null hypothesis = 0 and alpha = 0.05), 41.73%
#> of the estimate of -2.2 would have to be due to bias. This implies that to
#> nullify the inference one would expect to have to replace 83 (41.73%)
#> observations with data points for which the effect is 0 (RIR = 83).
#>
#> See Frank et al. (2013) for a description of the method.
#>
#> Citation: Frank, K.A., Maroulis, S., Duong, M., and Kelcey, B. (2013).
#> What would it take to change an inference?
#> Using Rubin's causal model to interpret the robustness of causal inferences.
#> Education, Evaluation and Policy Analysis, 35 437-460.
#>
#> Accuracy of results increases with the number of decimals reported.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(.5, 3, 200, 3)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 183
#>
#> The estimated effect is 0.5. The threshold value for statistical significance
#> is 5.917 (with null hypothesis = 0 and alpha = 0.05). To reach that threshold,
#> 91.549% of the estimate of 0.5 would have to be due to bias. This implies to sustain
#> an inference one would expect to have to replace 183 (91.549%) observations with
#> effect of 0 with data points with effect of 5.917 (RIR = 183).
#>
#> See Frank et al. (2013) for a description of the method.
#>
#> Citation: Frank, K.A., Maroulis, S., Duong, M., and Kelcey, B. (2013).
#> What would it take to change an inference?
#> Using Rubin's causal model to interpret the robustness of causal inferences.
#> Education, Evaluation and Policy Analysis, 35 437-460.
#>
#> Accuracy of results increases with the number of decimals reported.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(-0.2, 0.103, 20888, 3, n_treat = 17888, model_type = "logistic")
#> Robustness of Inference to Replacement (RIR):
#> RIR = 2
#> Fragility = 1
#>
#> You entered: log odds = -0.200, SE = 0.103, with p-value = 0.052.
#> The table implied by the parameter estimates and sample sizes you entered:
#>
#> Implied Table:
#> Fail Success Success_Rate
#> Control 2882 118 3.93%
#> Treatment 17308 580 3.24%
#> Total 20190 698 3.34%
#>
#> Values in the table have been rounded to the nearest integer. This may cause
#> a small change to the estimated effect for the table.
#>
#> To sustain an inference that the effect is different from 0 (alpha = 0.050), one would
#> need to transfer 1 data points from treatment success to treatment failure (Fragility = 1).
#> This is equivalent to replacing 2 (0.345%) treatment success data points with data points
#> for which the probability of failure in the control group (96.067%) applies (RIR = 2).
#>
#> Note that RIR = Fragility/P(destination) = 1/0.961 ~ 2.
#>
#> The transfer of 1 data points yields the following table:
#>
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 2882 118 3.93%
#> Treatment 17309 579 3.24%
#> Total 20191 697 3.34%
#>
#> The log odds (estimated effect) = -0.202, SE = 0.103, p-value = 0.050.
#> This p-value is based on t = estimated effect/standard error
#>
#> Benchmarking RIR for Logistic Regression (Beta Version)
#> The treatment is not statistically significant in the implied table and would also not be
#> statistically significant in the raw table (before covariates were added). In this scenario, we
#> do not yet have a clear interpretation of the benchmark and therefore the benchmark calculation
#> is not reported.
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> Accuracy of results increases with the number of decimals entered.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
# using a confidence interval
pkonfound(upper_bound = 3, lower_bound = 1, n_obs = 100, n_covariates = 3)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 50
#>
#> To nullify the inference of an effect using the threshold of 1 for
#> statistical significance (with null hypothesis = 0 and alpha = 0.05), 49.987%
#> of the estimate of 2 would have to be due to bias. This implies that to
#> nullify the inference one would expect to have to replace 50 (49.987%)
#> observations with data points for which the effect is 0 (RIR = 50).
#>
#> See Frank et al. (2013) for a description of the method.
#>
#> Citation: Frank, K.A., Maroulis, S., Duong, M., and Kelcey, B. (2013).
#> What would it take to change an inference?
#> Using Rubin's causal model to interpret the robustness of causal inferences.
#> Education, Evaluation and Policy Analysis, 35 437-460.
#>
#> Accuracy of results increases with the number of decimals reported.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(2, .4, 100, 3, to_return = "thresh_plot")
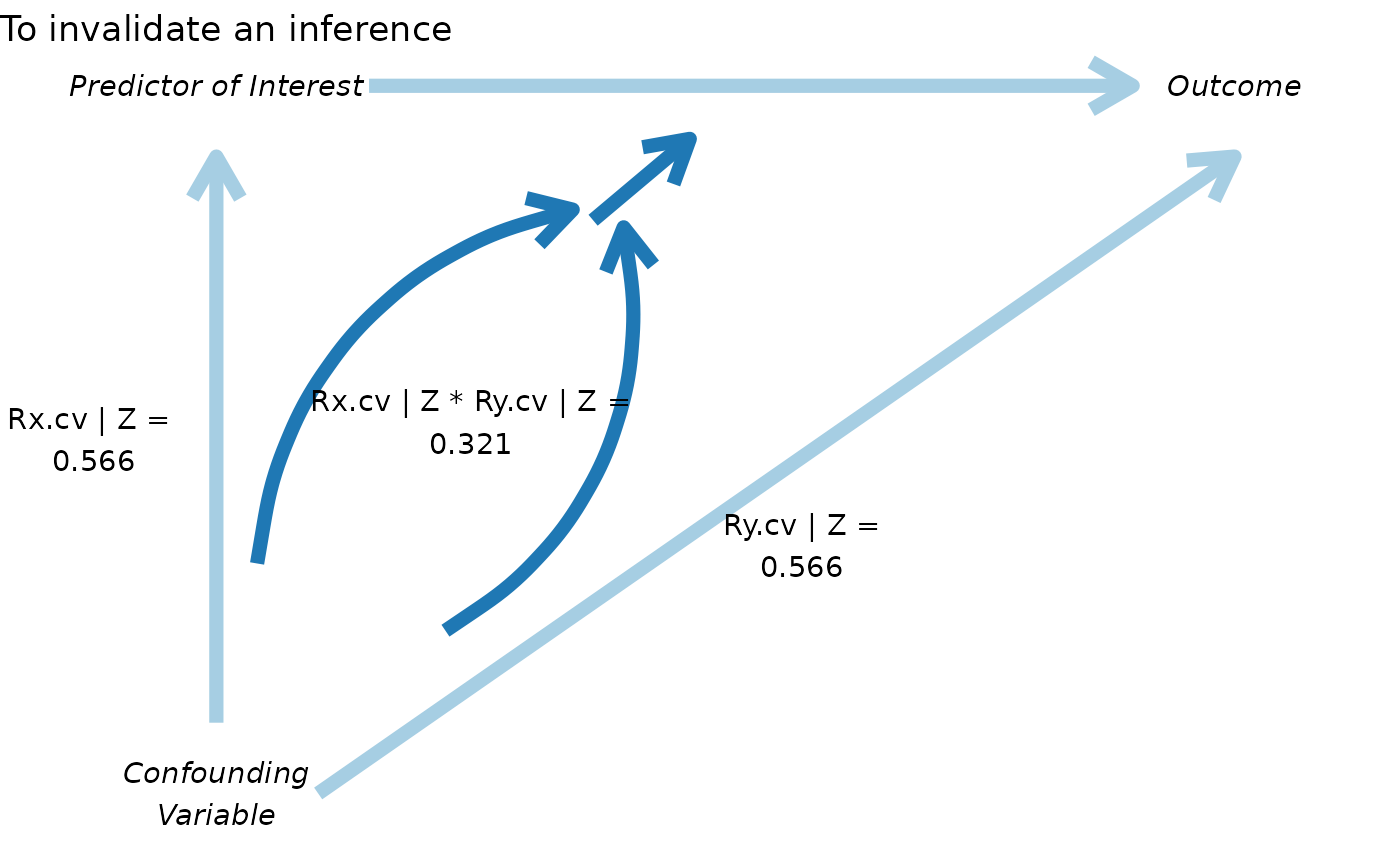
 pkonfound(2, .4, 100, 3, to_return = "corr_plot")
pkonfound(2, .4, 100, 3, to_return = "corr_plot")
 ## Logistic regression model example
pkonfound(-0.2, 0.103, 20888, 3, n_treat = 17888, model_type = "logistic")
#> Robustness of Inference to Replacement (RIR):
#> RIR = 2
#> Fragility = 1
#>
#> You entered: log odds = -0.200, SE = 0.103, with p-value = 0.052.
#> The table implied by the parameter estimates and sample sizes you entered:
#>
#> Implied Table:
#> Fail Success Success_Rate
#> Control 2882 118 3.93%
#> Treatment 17308 580 3.24%
#> Total 20190 698 3.34%
#>
#> Values in the table have been rounded to the nearest integer. This may cause
#> a small change to the estimated effect for the table.
#>
#> To sustain an inference that the effect is different from 0 (alpha = 0.050), one would
#> need to transfer 1 data points from treatment success to treatment failure (Fragility = 1).
#> This is equivalent to replacing 2 (0.345%) treatment success data points with data points
#> for which the probability of failure in the control group (96.067%) applies (RIR = 2).
#>
#> Note that RIR = Fragility/P(destination) = 1/0.961 ~ 2.
#>
#> The transfer of 1 data points yields the following table:
#>
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 2882 118 3.93%
#> Treatment 17309 579 3.24%
#> Total 20191 697 3.34%
#>
#> The log odds (estimated effect) = -0.202, SE = 0.103, p-value = 0.050.
#> This p-value is based on t = estimated effect/standard error
#>
#> Benchmarking RIR for Logistic Regression (Beta Version)
#> The treatment is not statistically significant in the implied table and would also not be
#> statistically significant in the raw table (before covariates were added). In this scenario, we
#> do not yet have a clear interpretation of the benchmark and therefore the benchmark calculation
#> is not reported.
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> Accuracy of results increases with the number of decimals entered.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
## 2x2 table examples
pkonfound(a = 35, b = 17, c = 17, d = 38)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 14
#> Fragility = 9
#>
#> This function calculates the number of data points that would have to be replaced with
#> zero effect data points (RIR) to nullify the inference made about the association
#> between the rows and columns in a 2x2 table.
#> One can also interpret this as switches (Fragility) from one cell to another, such as from the
#> treatment success cell to the treatment failure cell.
#>
#> To nullify the inference that the effect is different from 0 (alpha = 0.05),
#> one would need to transfer 9 data points from treatment success to treatment failure as shown,
#> from the User-entered Table to the Transfer Table (Fragility = 9).
#> This is equivalent to replacing 14 (36.842%) treatment success data points with data points
#> for which the probability of failure in the control group (67.308%) applies (RIR = 14).
#>
#> RIR = Fragility/P(destination)
#>
#> For the User-entered Table, the estimated odds ratio is 4.530, with p-value of 0.000:
#> User-entered Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 17 38 69.09%
#> Total 52 55 51.40%
#>
#> For the Transfer Table, the estimated odds ratio is 2.278, with p-value of 0.051:
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 26 29 52.73%
#> Total 61 46 42.99%
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(a = 35, b = 17, c = 17, d = 38, alpha = 0.01)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 9
#> Fragility = 6
#>
#> This function calculates the number of data points that would have to be replaced with
#> zero effect data points (RIR) to nullify the inference made about the association
#> between the rows and columns in a 2x2 table.
#> One can also interpret this as switches (Fragility) from one cell to another, such as from the
#> treatment success cell to the treatment failure cell.
#>
#> To nullify the inference that the effect is different from 0 (alpha = 0.01),
#> one would need to transfer 6 data points from treatment success to treatment failure as shown,
#> from the User-entered Table to the Transfer Table (Fragility = 6).
#> This is equivalent to replacing 9 (23.684%) treatment success data points with data points
#> for which the probability of failure in the control group (67.308%) applies (RIR = 9).
#>
#> RIR = Fragility/P(destination)
#>
#> For the User-entered Table, the estimated odds ratio is 4.530, with p-value of 0.000:
#> User-entered Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 17 38 69.09%
#> Total 52 55 51.40%
#>
#> For the Transfer Table, the estimated odds ratio is 2.835, with p-value of 0.011:
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 23 32 58.18%
#> Total 58 49 45.79%
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(a = 35, b = 17, c = 17, d = 38, alpha = 0.01, switch_trm = FALSE)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 19
#> Fragility = 6
#>
#> This function calculates the number of data points that would have to be replaced with
#> zero effect data points (RIR) to nullify the inference made about the association
#> between the rows and columns in a 2x2 table.
#> One can also interpret this as switches (Fragility) from one cell to another, such as from the
#> treatment success cell to the treatment failure cell.
#>
#> To nullify the inference that the effect is different from 0 (alpha = 0.01),
#> one would need to transfer 6 data points from control failure to control success as shown,
#> from the User-entered Table to the Transfer Table (Fragility = 6).
#> This is equivalent to replacing 19 (54.286%) control failure data points with data points
#> for which the probability of success in the control group (32.692%) applies (RIR = 19).
#>
#> RIR = Fragility/P(destination)
#>
#> For the User-entered Table, the estimated odds ratio is 4.530, with p-value of 0.000:
#> User-entered Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 17 38 69.09%
#> Total 52 55 51.40%
#>
#> For the Transfer Table, the estimated odds ratio is 2.790, with p-value of 0.012:
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 29 23 44.23%
#> Treatment 17 38 69.09%
#> Total 46 61 57.01%
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(a = 35, b = 17, c = 17, d = 38, test = "chisq")
#> Robustness of Inference to Replacement (RIR):
#> RIR = 15
#> Fragility = 10
#>
#> This function calculates the number of data points that would have to be replaced with
#> zero effect data points (RIR) to nullify the inference made about the association
#> between the rows and columns in a 2x2 table.
#> One can also interpret this as switches (Fragility) from one cell to another, such as from the
#> treatment success cell to the treatment failure cell.
#>
#> To nullify the inference that the effect is different from 0 (alpha = 0.05),
#> one would need to transfer 10 data points from treatment success to treatment failure as shown,
#> from the User-entered Table to the Transfer Table (Fragility = 10).
#> This is equivalent to replacing 15 (39.474%) treatment success data points with data points
#> for which the probability of failure in the control group (67.308%) applies (RIR = 15).
#>
#> RIR = Fragility/P(destination)
#>
#> For the User-entered Table, the Pearson's chi square is 14.176, with p-value of 0.000:
#> User-entered Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 17 38 69.09%
#> Total 52 55 51.40%
#>
#> For the Transfer Table, the Pearson's chi square is 3.640, with p-value of 0.056:
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 27 28 50.91%
#> Total 62 45 42.06%
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
## Advanced examples
# Calculating unconditional ITCV and benchmark correlation for ITCV
pkonfound(est_eff = .5, std_err = .056, n_obs = 6174, sdx = 0.22, sdy = 1, R2 = .3,
index = "IT", to_return = "print")
#> Impact Threshold for a Confounding Variable (ITCV):
#> Unconditional ITCV:
#> The minimum impact of an omitted variable to nullify an inference for
#> a null hypothesis of an effect of 0 (nu) is based on a correlation of 0.253
#> with the outcome and 0.26 with the predictor of interest (BEFORE conditioning
#> on observed covariates; signs are interchangeable if they are different).
#> This is based on a threshold effect of 0.025 for statistical significance (alpha = 0.05).
#>
#> Correspondingly the UNCONDITIONAL impact of an omitted variable (as defined in Frank 2000) must be
#> 0.253 X 0.26 = 0.066 to nullify an inference for a null hypothesis of an effect of 0 (nu).
#>
#> Conditional ITCV:
#> The minimum impact of an omitted variable to nullify an inference for
#> a null hypothesis of an effect of 0 (nu) is based on a correlation of 0.3
#> with the outcome and 0.3 with the predictor of interest (conditioning on all
#> observed covariates in the model; signs are interchangeable if they are different).
#> This is based on a threshold effect of 0.025 for statistical significance (alpha = 0.05).
#>
#> Correspondingly the conditional impact of an omitted variable (as defined in Frank 2000) must be
#> 0.3 X 0.3 = 0.09 to nullify an inference for a null hypothesis of an effect of 0 (nu).
#>
#> Interpretation of Benchmark Correlations for ITCV:
#> Benchmark correlation product ('benchmark_corr_product') is Rxz*Ryz = 0.0735, showing
#> the association strength of all observed covariates Z with X and Y.
#>
#> The ratio ('itcv_ratio_to_benchmark') is unconditional ITCV/Benchmark = 0.0657/0.0735 = 0.8936.
#>
#> The larger the ratio the stronger must be the unobserved impact relative to the
#> impact of all observed covariates to nullify the inference. The larger the ratio
#> the more robust the inference.
#>
#> If Z includes pretests or fixed effects, the benchmark may be inflated, making the ratio
#> unusually small. Interpret robustness cautiously in such cases.
#>
#> See Frank (2000) for a description of the method.
#>
#> Citation:
#> Frank, K. (2000). Impact of a confounding variable on the inference of a
#> regression coefficient. Sociological Methods and Research, 29 (2), 147-194
#>
#> Accuracy of results increases with the number of decimals reported.
#>
#> The ITCV analysis was originally derived for OLS standard errors. If the
#> standard errors reported in the table were not based on OLS, some caution
#> should be used to interpret the ITCV.
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
# Calculating delta* and delta_exact
pkonfound(est_eff = .4, std_err = .1, n_obs = 290, sdx = 2, sdy = 6, R2 = .7,
eff_thr = 0, FR2max = .8, index = "COP", to_return = "raw_output")
#> $`delta*`
#> [1] 3.668243
#>
#> $`delta*restricted`
#> [1] 4.085172
#>
#> $delta_Correlation
#> [1] 1.508536
#>
#> $delta_pctbias
#> [1] 143.1658
#>
#> $delta_sig
#> [1] 0.9300026
#>
#> $rxcvGz_sig
#> [1] 0.2333602
#>
#> $rycvGz_sig
#> [1] 0.6000109
#>
#> $cor_oster
#> Y X Z CV
#> Y 1.0000000 0.3266139 0.8266047 0.2579193
#> X 0.3266139 1.0000000 0.2433792 0.8659296
#> Z 0.8266047 0.2433792 1.0000000 0.0000000
#> CV 0.2579193 0.8659296 0.0000000 1.0000000
#>
#> $cor_exact
#> Y X Z CV
#> Y 1.0000000 0.3266139 0.8266047 0.3416500
#> X 0.3266139 1.0000000 0.2433792 0.3671463
#> Z 0.8266047 0.2433792 1.0000000 0.0000000
#> CV 0.3416500 0.3671463 0.0000000 1.0000000
#>
#> $`var(Y)`
#> [1] 36
#>
#> $`var(X)`
#> [1] 4
#>
#> $`var(CV)`
#> [1] 1
#>
#> $eff_x_M3_oster
#> [1] -1.538308
#>
#> $eff_x_M3
#> [1] -1.114065e-16
#>
#> $Table
#> M1:X M2:X,Z M3(delta_Correlation):X,Z,CV M3(delta*):X,Z,CV
#> R2 0.1097571 0.7008711 8.006897e-01 0.8006897
#> coef_X 0.9798418 0.3980344 -1.114065e-16 -1.5383085
#> SE_X 0.1665047 0.0995086 8.775619e-02 0.1803006
#> std_coef_X 0.3266139 0.2297940 0.000000e+00 -0.5127695
#> t_X 5.8847685 4.0000000 -1.269500e-15 -8.5319081
#> coef_CV NA NA 2.049900e+00 4.2116492
#> SE_CV NA NA 1.702349e-01 0.3497584
#> t_CV NA NA 1.204159e+01 12.0415946
#>
#> $Figure
#> Warning: Use of `figTable$coef_X` is discouraged.
#> ℹ Use `coef_X` instead.
#> Warning: Use of `figTable$ModelLabel` is discouraged.
#> ℹ Use `ModelLabel` instead.
#> Warning: Use of `figTable$ModelLabel` is discouraged.
#> ℹ Use `ModelLabel` instead.
#> Warning: Use of `figTable$ModelLabel` is discouraged.
#> ℹ Use `ModelLabel` instead.
#> Warning: Use of `figTable$coef_X` is discouraged.
#> ℹ Use `coef_X` instead.
#> Warning: Use of `figTable$ModelLabel` is discouraged.
#> ℹ Use `ModelLabel` instead.
## Logistic regression model example
pkonfound(-0.2, 0.103, 20888, 3, n_treat = 17888, model_type = "logistic")
#> Robustness of Inference to Replacement (RIR):
#> RIR = 2
#> Fragility = 1
#>
#> You entered: log odds = -0.200, SE = 0.103, with p-value = 0.052.
#> The table implied by the parameter estimates and sample sizes you entered:
#>
#> Implied Table:
#> Fail Success Success_Rate
#> Control 2882 118 3.93%
#> Treatment 17308 580 3.24%
#> Total 20190 698 3.34%
#>
#> Values in the table have been rounded to the nearest integer. This may cause
#> a small change to the estimated effect for the table.
#>
#> To sustain an inference that the effect is different from 0 (alpha = 0.050), one would
#> need to transfer 1 data points from treatment success to treatment failure (Fragility = 1).
#> This is equivalent to replacing 2 (0.345%) treatment success data points with data points
#> for which the probability of failure in the control group (96.067%) applies (RIR = 2).
#>
#> Note that RIR = Fragility/P(destination) = 1/0.961 ~ 2.
#>
#> The transfer of 1 data points yields the following table:
#>
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 2882 118 3.93%
#> Treatment 17309 579 3.24%
#> Total 20191 697 3.34%
#>
#> The log odds (estimated effect) = -0.202, SE = 0.103, p-value = 0.050.
#> This p-value is based on t = estimated effect/standard error
#>
#> Benchmarking RIR for Logistic Regression (Beta Version)
#> The treatment is not statistically significant in the implied table and would also not be
#> statistically significant in the raw table (before covariates were added). In this scenario, we
#> do not yet have a clear interpretation of the benchmark and therefore the benchmark calculation
#> is not reported.
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> Accuracy of results increases with the number of decimals entered.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
## 2x2 table examples
pkonfound(a = 35, b = 17, c = 17, d = 38)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 14
#> Fragility = 9
#>
#> This function calculates the number of data points that would have to be replaced with
#> zero effect data points (RIR) to nullify the inference made about the association
#> between the rows and columns in a 2x2 table.
#> One can also interpret this as switches (Fragility) from one cell to another, such as from the
#> treatment success cell to the treatment failure cell.
#>
#> To nullify the inference that the effect is different from 0 (alpha = 0.05),
#> one would need to transfer 9 data points from treatment success to treatment failure as shown,
#> from the User-entered Table to the Transfer Table (Fragility = 9).
#> This is equivalent to replacing 14 (36.842%) treatment success data points with data points
#> for which the probability of failure in the control group (67.308%) applies (RIR = 14).
#>
#> RIR = Fragility/P(destination)
#>
#> For the User-entered Table, the estimated odds ratio is 4.530, with p-value of 0.000:
#> User-entered Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 17 38 69.09%
#> Total 52 55 51.40%
#>
#> For the Transfer Table, the estimated odds ratio is 2.278, with p-value of 0.051:
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 26 29 52.73%
#> Total 61 46 42.99%
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(a = 35, b = 17, c = 17, d = 38, alpha = 0.01)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 9
#> Fragility = 6
#>
#> This function calculates the number of data points that would have to be replaced with
#> zero effect data points (RIR) to nullify the inference made about the association
#> between the rows and columns in a 2x2 table.
#> One can also interpret this as switches (Fragility) from one cell to another, such as from the
#> treatment success cell to the treatment failure cell.
#>
#> To nullify the inference that the effect is different from 0 (alpha = 0.01),
#> one would need to transfer 6 data points from treatment success to treatment failure as shown,
#> from the User-entered Table to the Transfer Table (Fragility = 6).
#> This is equivalent to replacing 9 (23.684%) treatment success data points with data points
#> for which the probability of failure in the control group (67.308%) applies (RIR = 9).
#>
#> RIR = Fragility/P(destination)
#>
#> For the User-entered Table, the estimated odds ratio is 4.530, with p-value of 0.000:
#> User-entered Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 17 38 69.09%
#> Total 52 55 51.40%
#>
#> For the Transfer Table, the estimated odds ratio is 2.835, with p-value of 0.011:
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 23 32 58.18%
#> Total 58 49 45.79%
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(a = 35, b = 17, c = 17, d = 38, alpha = 0.01, switch_trm = FALSE)
#> Robustness of Inference to Replacement (RIR):
#> RIR = 19
#> Fragility = 6
#>
#> This function calculates the number of data points that would have to be replaced with
#> zero effect data points (RIR) to nullify the inference made about the association
#> between the rows and columns in a 2x2 table.
#> One can also interpret this as switches (Fragility) from one cell to another, such as from the
#> treatment success cell to the treatment failure cell.
#>
#> To nullify the inference that the effect is different from 0 (alpha = 0.01),
#> one would need to transfer 6 data points from control failure to control success as shown,
#> from the User-entered Table to the Transfer Table (Fragility = 6).
#> This is equivalent to replacing 19 (54.286%) control failure data points with data points
#> for which the probability of success in the control group (32.692%) applies (RIR = 19).
#>
#> RIR = Fragility/P(destination)
#>
#> For the User-entered Table, the estimated odds ratio is 4.530, with p-value of 0.000:
#> User-entered Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 17 38 69.09%
#> Total 52 55 51.40%
#>
#> For the Transfer Table, the estimated odds ratio is 2.790, with p-value of 0.012:
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 29 23 44.23%
#> Treatment 17 38 69.09%
#> Total 46 61 57.01%
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
pkonfound(a = 35, b = 17, c = 17, d = 38, test = "chisq")
#> Robustness of Inference to Replacement (RIR):
#> RIR = 15
#> Fragility = 10
#>
#> This function calculates the number of data points that would have to be replaced with
#> zero effect data points (RIR) to nullify the inference made about the association
#> between the rows and columns in a 2x2 table.
#> One can also interpret this as switches (Fragility) from one cell to another, such as from the
#> treatment success cell to the treatment failure cell.
#>
#> To nullify the inference that the effect is different from 0 (alpha = 0.05),
#> one would need to transfer 10 data points from treatment success to treatment failure as shown,
#> from the User-entered Table to the Transfer Table (Fragility = 10).
#> This is equivalent to replacing 15 (39.474%) treatment success data points with data points
#> for which the probability of failure in the control group (67.308%) applies (RIR = 15).
#>
#> RIR = Fragility/P(destination)
#>
#> For the User-entered Table, the Pearson's chi square is 14.176, with p-value of 0.000:
#> User-entered Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 17 38 69.09%
#> Total 52 55 51.40%
#>
#> For the Transfer Table, the Pearson's chi square is 3.640, with p-value of 0.056:
#> Transfer Table:
#> Fail Success Success_Rate
#> Control 35 17 32.69%
#> Treatment 27 28 50.91%
#> Total 62 45 42.06%
#>
#> See Frank et al. (2021) for a description of the methods.
#>
#> *Frank, K. A., *Lin, Q., *Maroulis, S., *Mueller, A. S., Xu, R., Rosenberg, J. M., ... & Zhang, L. (2021).
#> Hypothetical case replacement can be used to quantify the robustness of trial results. Journal of Clinical
#> Epidemiology, 134, 150-159.
#> *authors are listed alphabetically.
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
## Advanced examples
# Calculating unconditional ITCV and benchmark correlation for ITCV
pkonfound(est_eff = .5, std_err = .056, n_obs = 6174, sdx = 0.22, sdy = 1, R2 = .3,
index = "IT", to_return = "print")
#> Impact Threshold for a Confounding Variable (ITCV):
#> Unconditional ITCV:
#> The minimum impact of an omitted variable to nullify an inference for
#> a null hypothesis of an effect of 0 (nu) is based on a correlation of 0.253
#> with the outcome and 0.26 with the predictor of interest (BEFORE conditioning
#> on observed covariates; signs are interchangeable if they are different).
#> This is based on a threshold effect of 0.025 for statistical significance (alpha = 0.05).
#>
#> Correspondingly the UNCONDITIONAL impact of an omitted variable (as defined in Frank 2000) must be
#> 0.253 X 0.26 = 0.066 to nullify an inference for a null hypothesis of an effect of 0 (nu).
#>
#> Conditional ITCV:
#> The minimum impact of an omitted variable to nullify an inference for
#> a null hypothesis of an effect of 0 (nu) is based on a correlation of 0.3
#> with the outcome and 0.3 with the predictor of interest (conditioning on all
#> observed covariates in the model; signs are interchangeable if they are different).
#> This is based on a threshold effect of 0.025 for statistical significance (alpha = 0.05).
#>
#> Correspondingly the conditional impact of an omitted variable (as defined in Frank 2000) must be
#> 0.3 X 0.3 = 0.09 to nullify an inference for a null hypothesis of an effect of 0 (nu).
#>
#> Interpretation of Benchmark Correlations for ITCV:
#> Benchmark correlation product ('benchmark_corr_product') is Rxz*Ryz = 0.0735, showing
#> the association strength of all observed covariates Z with X and Y.
#>
#> The ratio ('itcv_ratio_to_benchmark') is unconditional ITCV/Benchmark = 0.0657/0.0735 = 0.8936.
#>
#> The larger the ratio the stronger must be the unobserved impact relative to the
#> impact of all observed covariates to nullify the inference. The larger the ratio
#> the more robust the inference.
#>
#> If Z includes pretests or fixed effects, the benchmark may be inflated, making the ratio
#> unusually small. Interpret robustness cautiously in such cases.
#>
#> See Frank (2000) for a description of the method.
#>
#> Citation:
#> Frank, K. (2000). Impact of a confounding variable on the inference of a
#> regression coefficient. Sociological Methods and Research, 29 (2), 147-194
#>
#> Accuracy of results increases with the number of decimals reported.
#>
#> The ITCV analysis was originally derived for OLS standard errors. If the
#> standard errors reported in the table were not based on OLS, some caution
#> should be used to interpret the ITCV.
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
# Calculating delta* and delta_exact
pkonfound(est_eff = .4, std_err = .1, n_obs = 290, sdx = 2, sdy = 6, R2 = .7,
eff_thr = 0, FR2max = .8, index = "COP", to_return = "raw_output")
#> $`delta*`
#> [1] 3.668243
#>
#> $`delta*restricted`
#> [1] 4.085172
#>
#> $delta_Correlation
#> [1] 1.508536
#>
#> $delta_pctbias
#> [1] 143.1658
#>
#> $delta_sig
#> [1] 0.9300026
#>
#> $rxcvGz_sig
#> [1] 0.2333602
#>
#> $rycvGz_sig
#> [1] 0.6000109
#>
#> $cor_oster
#> Y X Z CV
#> Y 1.0000000 0.3266139 0.8266047 0.2579193
#> X 0.3266139 1.0000000 0.2433792 0.8659296
#> Z 0.8266047 0.2433792 1.0000000 0.0000000
#> CV 0.2579193 0.8659296 0.0000000 1.0000000
#>
#> $cor_exact
#> Y X Z CV
#> Y 1.0000000 0.3266139 0.8266047 0.3416500
#> X 0.3266139 1.0000000 0.2433792 0.3671463
#> Z 0.8266047 0.2433792 1.0000000 0.0000000
#> CV 0.3416500 0.3671463 0.0000000 1.0000000
#>
#> $`var(Y)`
#> [1] 36
#>
#> $`var(X)`
#> [1] 4
#>
#> $`var(CV)`
#> [1] 1
#>
#> $eff_x_M3_oster
#> [1] -1.538308
#>
#> $eff_x_M3
#> [1] -1.114065e-16
#>
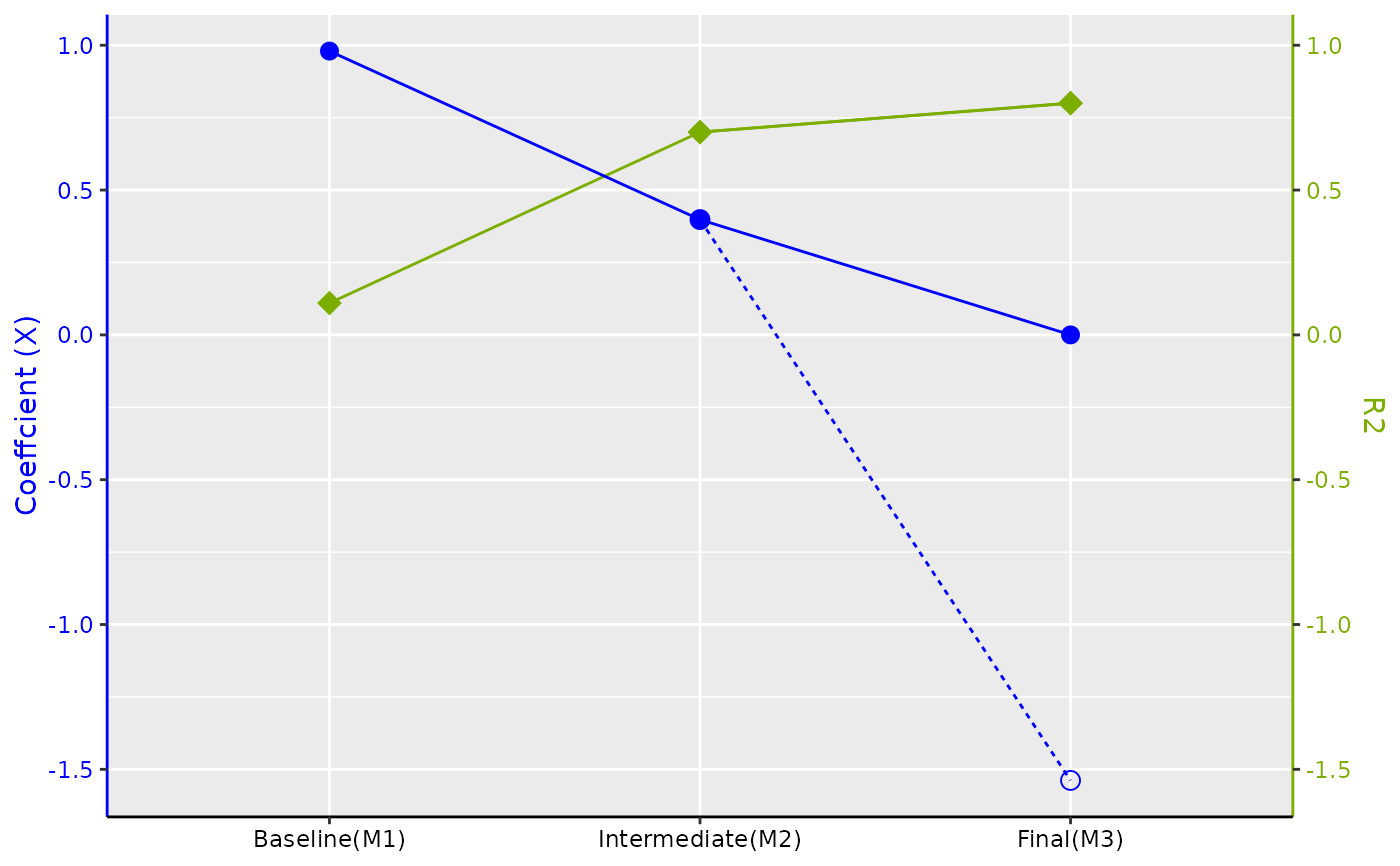
#> $Table
#> M1:X M2:X,Z M3(delta_Correlation):X,Z,CV M3(delta*):X,Z,CV
#> R2 0.1097571 0.7008711 8.006897e-01 0.8006897
#> coef_X 0.9798418 0.3980344 -1.114065e-16 -1.5383085
#> SE_X 0.1665047 0.0995086 8.775619e-02 0.1803006
#> std_coef_X 0.3266139 0.2297940 0.000000e+00 -0.5127695
#> t_X 5.8847685 4.0000000 -1.269500e-15 -8.5319081
#> coef_CV NA NA 2.049900e+00 4.2116492
#> SE_CV NA NA 1.702349e-01 0.3497584
#> t_CV NA NA 1.204159e+01 12.0415946
#>
#> $Figure
#> Warning: Use of `figTable$coef_X` is discouraged.
#> ℹ Use `coef_X` instead.
#> Warning: Use of `figTable$ModelLabel` is discouraged.
#> ℹ Use `ModelLabel` instead.
#> Warning: Use of `figTable$ModelLabel` is discouraged.
#> ℹ Use `ModelLabel` instead.
#> Warning: Use of `figTable$ModelLabel` is discouraged.
#> ℹ Use `ModelLabel` instead.
#> Warning: Use of `figTable$coef_X` is discouraged.
#> ℹ Use `coef_X` instead.
#> Warning: Use of `figTable$ModelLabel` is discouraged.
#> ℹ Use `ModelLabel` instead.
 #>
# Calculating rxcv and rycv when preserving standard error
pkonfound(est_eff = .5, std_err = .056, n_obs = 6174, eff_thr = .1,
sdx = 0.22, sdy = 1, R2 = .3, index = "PSE", to_return = "raw_output")
#> $`correlation between X and CV conditional on Z`
#> [1] 0.2479732
#>
#> $`correlation between Y and CV conditional on Z`
#> [1] 0.3721927
#>
#> $`correlation between X and CV`
#> [1] 0.2143707
#>
#> $`correlation between Y and CV`
#> [1] 0.313404
#>
#> $`covariance matrix`
#> Y X Z CV
#> Y 1.00000000 0.07773579 0.5394031 0.31340398
#> X 0.07773579 0.04840000 0.1105826 0.04716155
#> Z 0.53940306 0.11058258 1.0000000 0.00000000
#> CV 0.31340398 0.04716155 0.0000000 1.00000000
#>
#> $eff_M3
#> [1] 0.09740386
#>
#> $se_M3
#> [1] 0.05397058
#>
#> $Table
#> M1:X M2:X,Z M3:X,Z,CV
#> R2 0.12499409 0.30011338 0.38959867
#> coef_X 1.60611143 0.50004052 0.09740386
#> SE_X 0.05411712 0.05598639 0.05397058
#> std_coef_X 0.35334452 0.11294102 0.02142885
#> t_X 29.67843530 8.93146515 1.80475837
#> coef_Z NA 0.48410729 0.52863189
#> SE_Z NA 0.01231701 0.01159750
#> t_Z NA 39.30397315 45.58155174
#> coef_CV NA NA 0.30881026
#> SE_CV NA NA 0.01026456
#> t_CV NA NA 30.08509668
#>
#> $RIR_perc
#> [1] 0.7861584
#>
#> $`standard deviation of unobserved Y`
#> [1] 0.9591486
#>
# VAM beta
pkonfound(est_eff = 0.14, replace_stu = 0.16, n_obs = 20, eff_thr = 0.15,
peer_effect_pi = 0.3, index = "VAM")
#> This is beta version of the VAM function.
#>
#> The reported VAM score is 0.140 with evaluation threshold of 0.15. The VAM score is below the threshold. Therefore, the RIR indicates replacement required to increase the VAM above the threshold.
#>
#> If there are no peer effects, then 10 (50%) students must be replaced with students whose score is 0.16 (as specified) to move the VAM above the threshold (RIR = 50% * 20 = 10).
#>
#> If all of the bias comes from peer spillover effects, and we assume 30% (as specified) students are distracting the others, then a peer effect of 0.002 is needed to change the evaluation. Each replaced student must have a -0.002 effect (compared to their replacements) on each of the non-replaced students to cross the threshold for evaluation.
#>
#> See the figure for combinations of size of peer effect by proportion to be replaced (pi) to change the evaluation. The red point marks the value reported above.
#>
#> The calculations and interpretation depend on your VAM model specification and estimation. See the paper for more details.
#>
#>
# Calculating rxcv and rycv when preserving standard error
pkonfound(est_eff = .5, std_err = .056, n_obs = 6174, eff_thr = .1,
sdx = 0.22, sdy = 1, R2 = .3, index = "PSE", to_return = "raw_output")
#> $`correlation between X and CV conditional on Z`
#> [1] 0.2479732
#>
#> $`correlation between Y and CV conditional on Z`
#> [1] 0.3721927
#>
#> $`correlation between X and CV`
#> [1] 0.2143707
#>
#> $`correlation between Y and CV`
#> [1] 0.313404
#>
#> $`covariance matrix`
#> Y X Z CV
#> Y 1.00000000 0.07773579 0.5394031 0.31340398
#> X 0.07773579 0.04840000 0.1105826 0.04716155
#> Z 0.53940306 0.11058258 1.0000000 0.00000000
#> CV 0.31340398 0.04716155 0.0000000 1.00000000
#>
#> $eff_M3
#> [1] 0.09740386
#>
#> $se_M3
#> [1] 0.05397058
#>
#> $Table
#> M1:X M2:X,Z M3:X,Z,CV
#> R2 0.12499409 0.30011338 0.38959867
#> coef_X 1.60611143 0.50004052 0.09740386
#> SE_X 0.05411712 0.05598639 0.05397058
#> std_coef_X 0.35334452 0.11294102 0.02142885
#> t_X 29.67843530 8.93146515 1.80475837
#> coef_Z NA 0.48410729 0.52863189
#> SE_Z NA 0.01231701 0.01159750
#> t_Z NA 39.30397315 45.58155174
#> coef_CV NA NA 0.30881026
#> SE_CV NA NA 0.01026456
#> t_CV NA NA 30.08509668
#>
#> $RIR_perc
#> [1] 0.7861584
#>
#> $`standard deviation of unobserved Y`
#> [1] 0.9591486
#>
# VAM beta
pkonfound(est_eff = 0.14, replace_stu = 0.16, n_obs = 20, eff_thr = 0.15,
peer_effect_pi = 0.3, index = "VAM")
#> This is beta version of the VAM function.
#>
#> The reported VAM score is 0.140 with evaluation threshold of 0.15. The VAM score is below the threshold. Therefore, the RIR indicates replacement required to increase the VAM above the threshold.
#>
#> If there are no peer effects, then 10 (50%) students must be replaced with students whose score is 0.16 (as specified) to move the VAM above the threshold (RIR = 50% * 20 = 10).
#>
#> If all of the bias comes from peer spillover effects, and we assume 30% (as specified) students are distracting the others, then a peer effect of 0.002 is needed to change the evaluation. Each replaced student must have a -0.002 effect (compared to their replacements) on each of the non-replaced students to cross the threshold for evaluation.
#>
#> See the figure for combinations of size of peer effect by proportion to be replaced (pi) to change the evaluation. The red point marks the value reported above.
#>
#> The calculations and interpretation depend on your VAM model specification and estimation. See the paper for more details.
#>
 #>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().
#>
#> For more information, visit https://konfound-it.org
#> To explore examples and interpretation tips,
#> see our Practical Guide at https://konfound-it.org/page/guide/
#>
#> For other forms of output, run
#> ?pkonfound and inspect the to_return argument
#> For models fit in R, consider use of konfound().